Conference papers

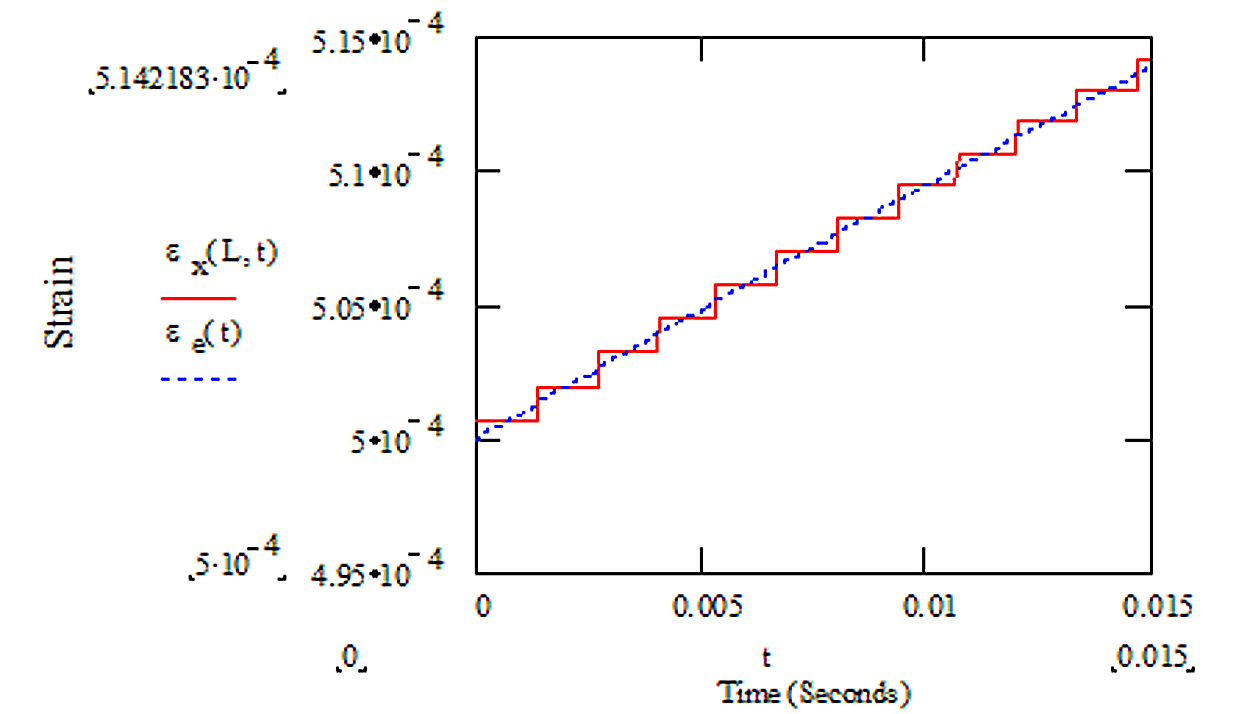
A Unified Model for Longitudinal and Lateral Web Dynamics IWEB 2019 PowerPoint Paper

In “The Effect of Mass Transfer on Multi-Span Lateral Dynamics of Uniform Webs”, it is shown that behavior of Shelton’s lateral dynamic beam model can be explained as the interaction of the normal entry equation and mass transfer between spans. The implications of mass transfer are discussed further in “The Connection Between Longitudinal and lateral Web Dynamics”.
In this paper, the mass transfer idea is generalized and used to develop a dynamic model that combines lateral and longitudinal (tension) behavior. Nonlinear elasticity theory is used to model the web as a two-dimensional membrane in a state of plane stress. Boundary conditions at the downstream roller are: 1) the normal entry equation, used in lateral models, and 2) the continuity equation, used in tension models.

Validity of the new model is tested by comparing its predictions with the results of numerous experiments documented in John Shelton's 1968 Dissertation.

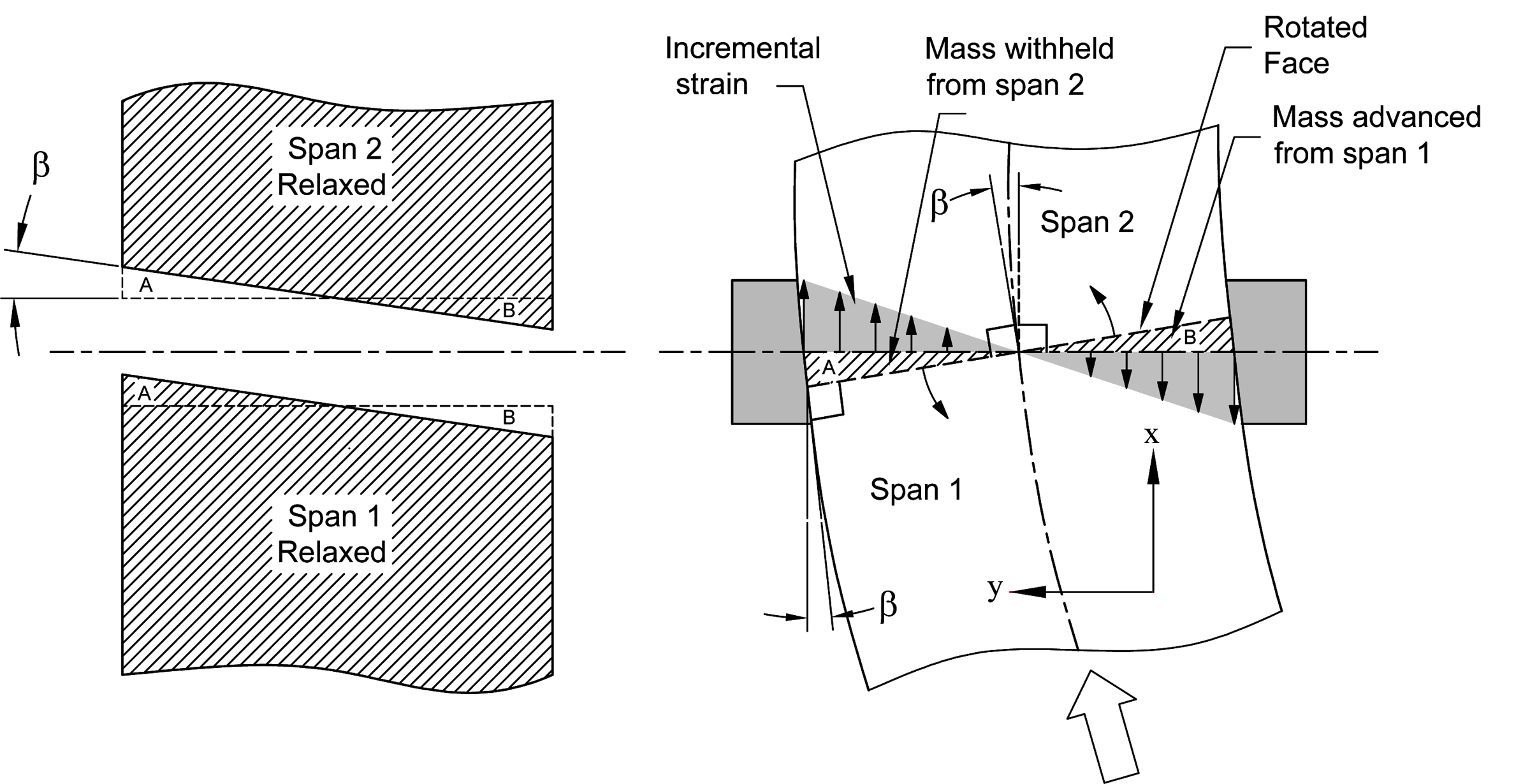
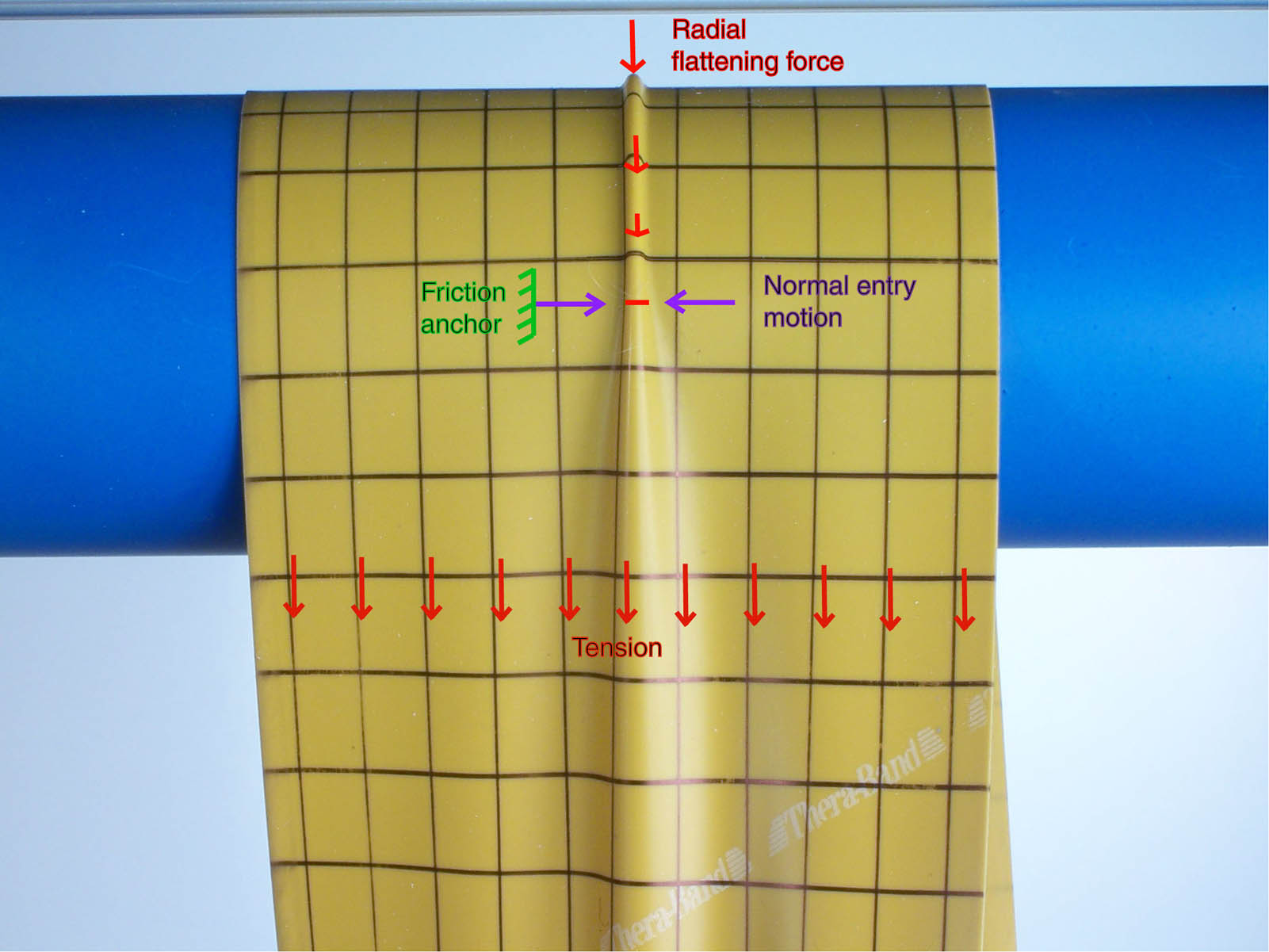
The Connection Between Longitudinal and Lateral Web Dynamics IWEB 2019 PowerPoint Paper

Where does the entry angle come from? This paper shows that the answer to this question reveals a connection between longitudinal and lateral behavior that has gone largely unnoticed.
In beam models, entry angle refers to the angle between the tangent to the web centerline and the normal to the roller axis at the line of entry onto the roller. Whenever the entry angle becomes non-zero, a web that is moving longitudinally through a process will also move laterally on the roller in a direction that returns the entry angle to zero. If the web is modeled as a perfectly flexible string, this behavior is intuitively obvious because it bends sharply on entering a roller that is pivoted or shifted laterally. However, in the case of the most commonly used Euler-Bernoulli (E-B) beam model, the web can’t make a sharp bend. If it is initially perpendicular to the roller axis, Bernoulli beam theory says that, provided there is no slipping, it should remain perpendicular as the roller is shifted or pivoted and thus wouldn’t move relative to the roller. We know from experience, however, that a real moving web begins to move laterally on the roller soon after it pivots or shifts. So, how is it that a Bernoulli beam model works so well?

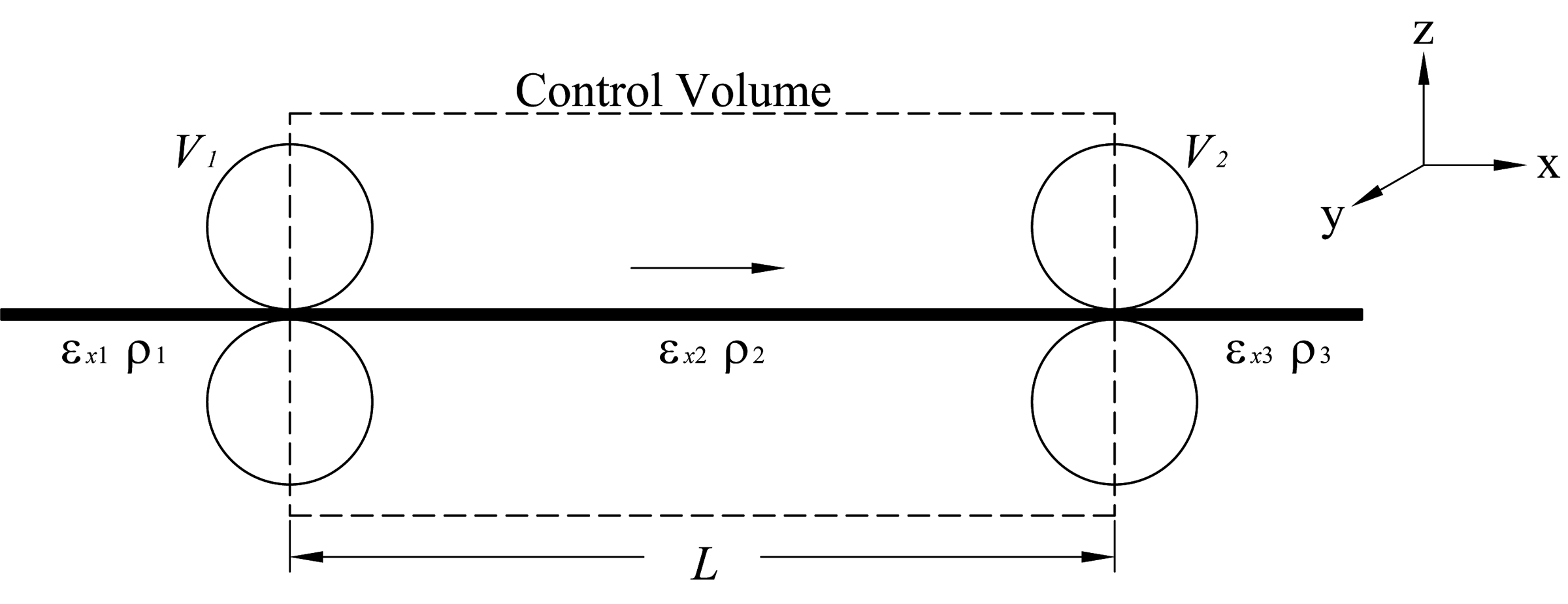
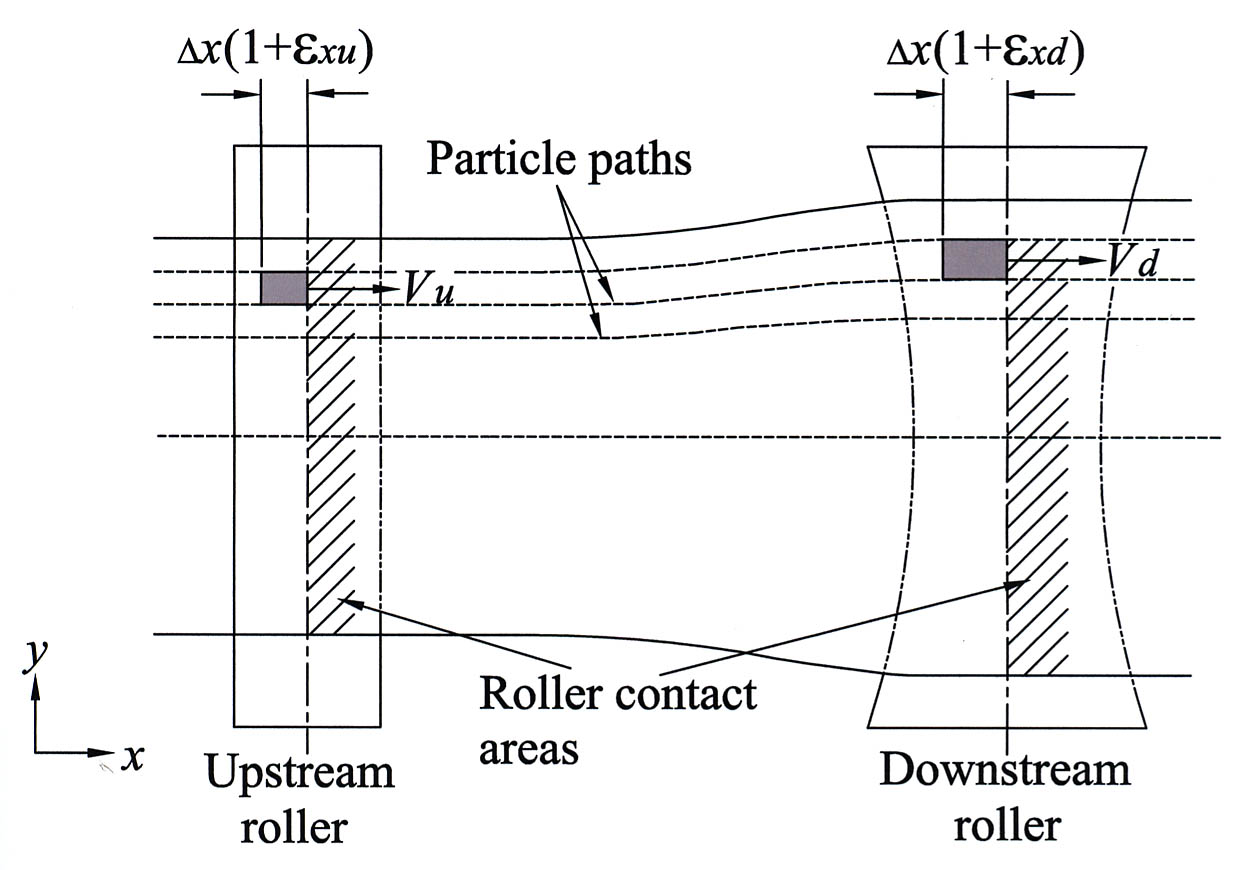
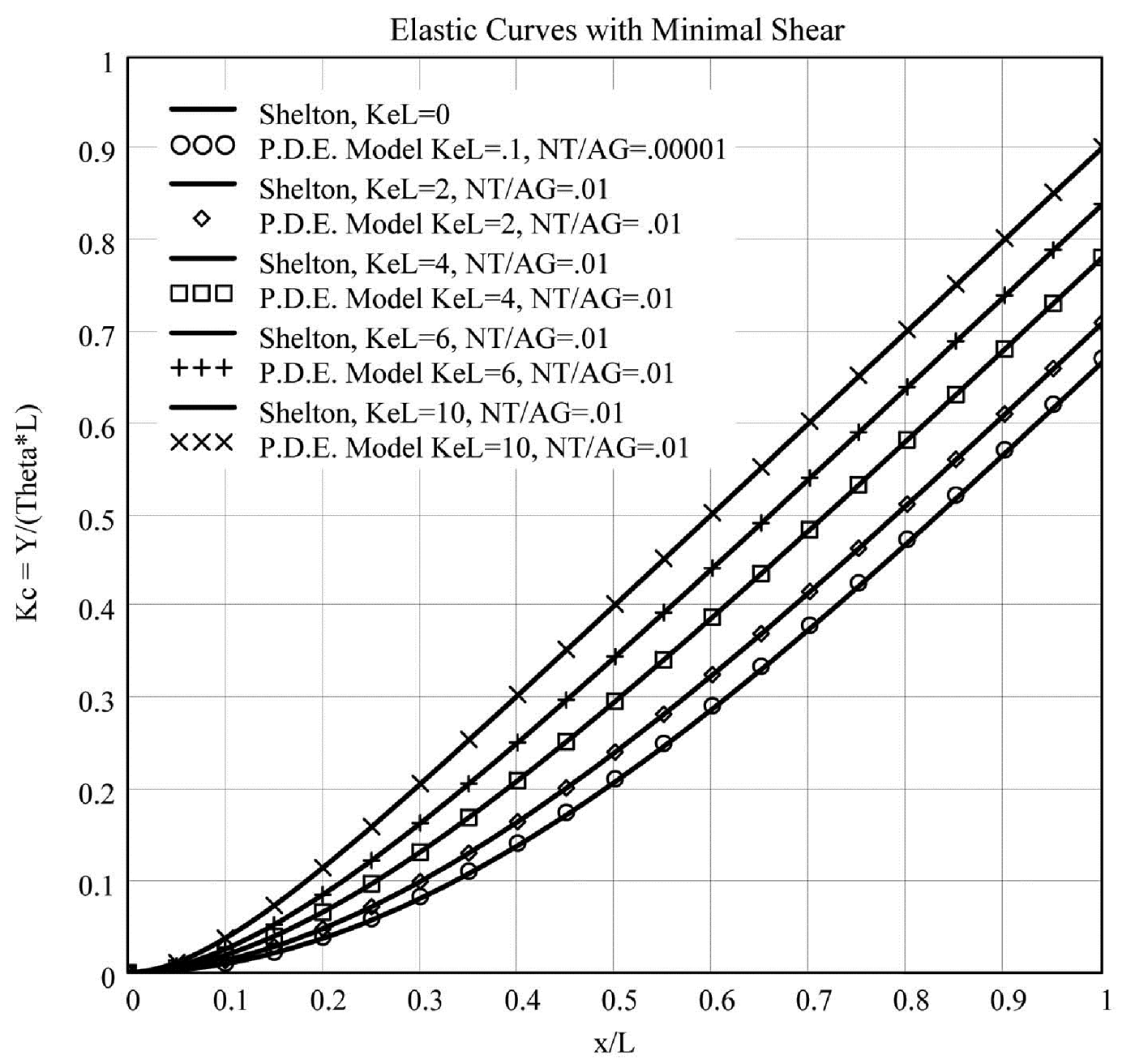
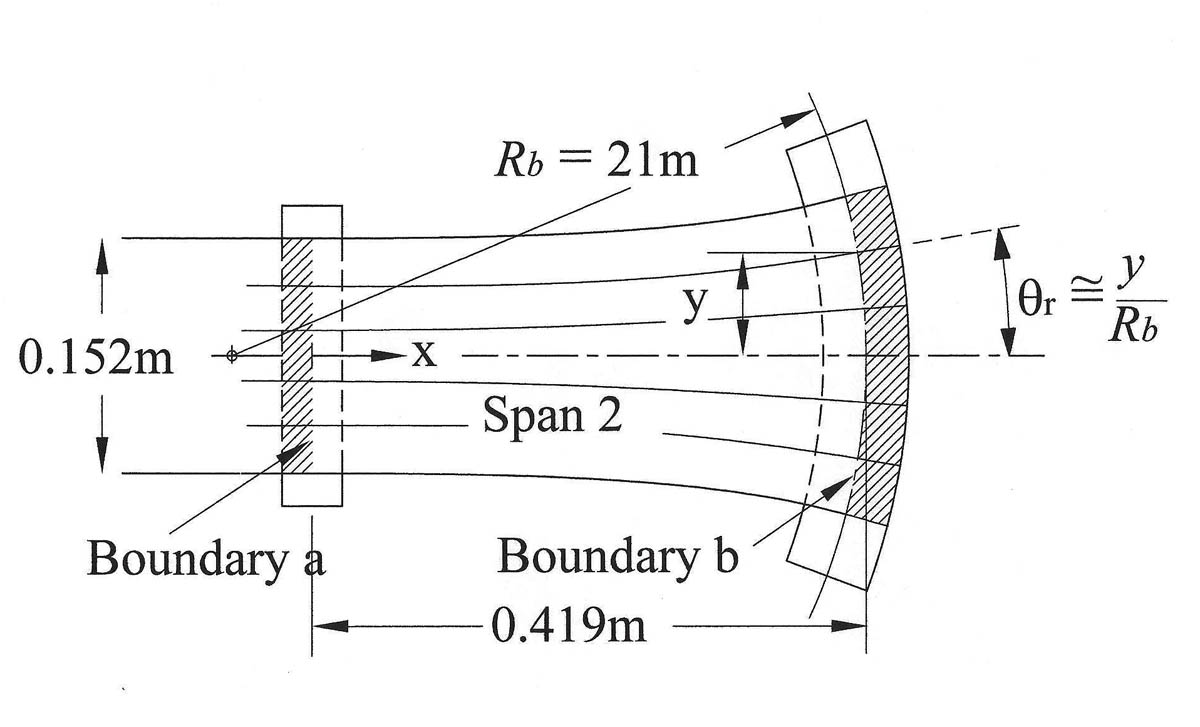
The effect of Mass Transfer on Multi-Span Lateral Dynamics of Uniform Webs IWEB 2017 PowerPoint Paper

This paper shows that the acceleration equation used in early multi-span lateral dynamic models is a consequence of mass transfer between spans . Mass transfer effects fully account for the equation currently used in Euler-Bernoulli models and provides an analytical pathway to the first beam model that correctly incorporates shear deformation by explicitly recognizing the role of mass transfer. It also ties together contributions from three other researchers – John Shelton, who pioneered the use of beam theory in models of lateral web dynamics, Lisa Sievers, who proposed the principle of continuity of bending angle and Richard Benson, who was the first to publish an acceleration equation that correctly incorporates shear deformation.

How Accurately Can I Guide My Web? AIMCAL 2015 PowerPoint Paper

Introduces fundamental concepts of lateral web control and explains three different ways that lateral errors can be regenerated downstream of a web guiding system. Based on work described in IWEB 2015 paper.

A Belated Appreciation of Lisa Sievers' Thesis IWEB 2015 PowerPoint Paper

In her 1987 thesis, Lisa Sievers described three multi-span dynamic models for lateral web behavior.

A convecting string with zero bending stiffness
Euler-Bernoulli beam with bending stiffness and no shear
Timoshenko beam with bending and shear

The last two transferred the bending deformation from one span to the next. Although Sievers shear model was incorrect, she built on the work of everyone before her, she creatively reanalyzed many aspects of beam analysis, putting it on a more rigorous mathematical footing. This deserves wider appreciation. In an effort to make the results of her thesis more accessible, it is reviewed and the Timoshenko model is recast into a form which facilitates comparison with Euler-Bernoulli models in current use.

A Comparison of Multi-span Dynamics Models IWEB 2015 PowerPoint Paper

The original goal for this paper was to recast the Sievers Timoshenko model into the same analytical form as an Euler-Bernoulli model in current use, called the Young-Shelton-Kardamilas (YSK) method. A Timoshenko-type YSK model was developed, however it produces values for the curvature factor that don't make sense. After exhaustive troubleshooting, I finally concluded that there is something fundamentally wrong with the basic idea. This paper describes the work done to date so that others can contribute to it.

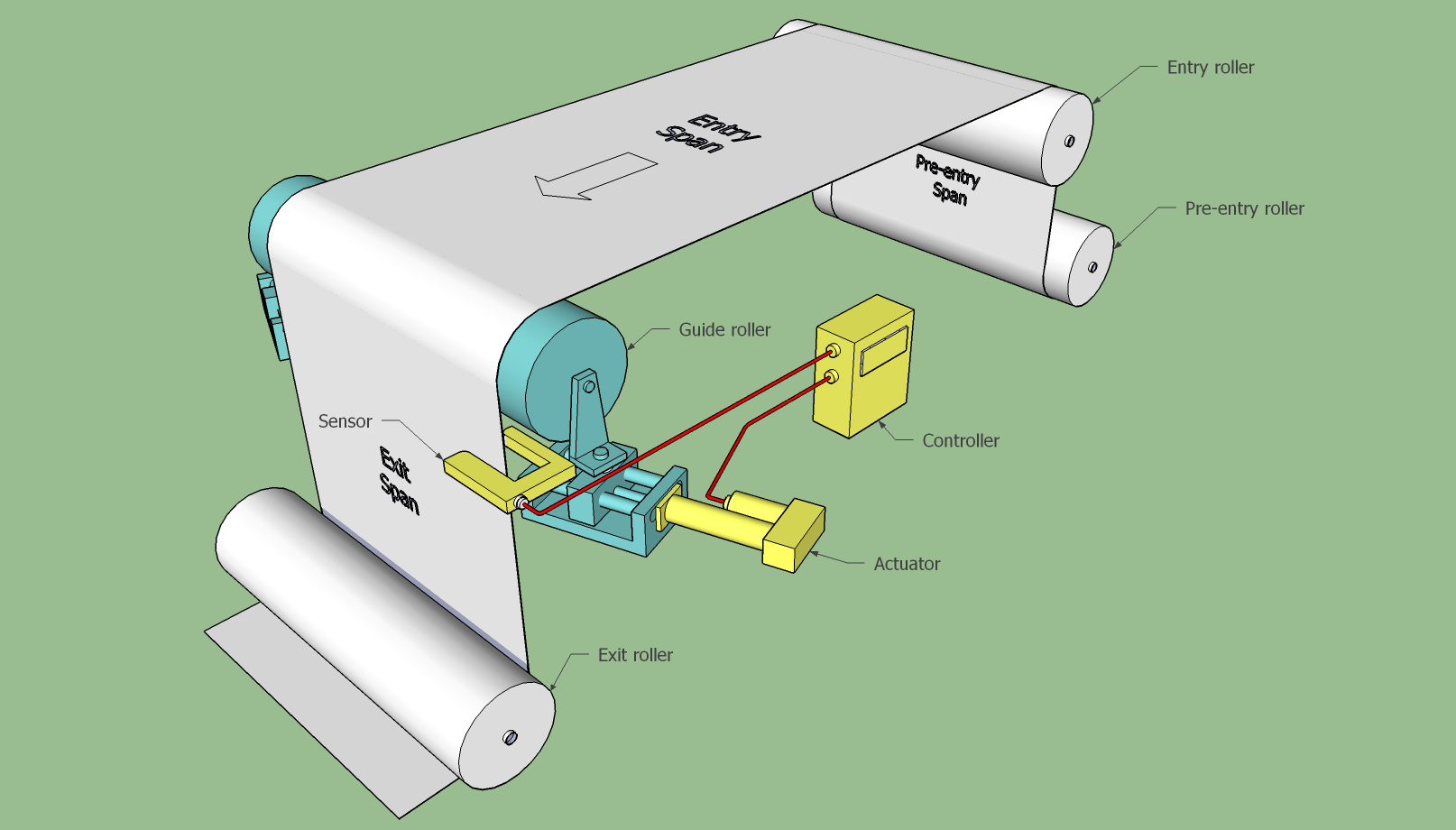
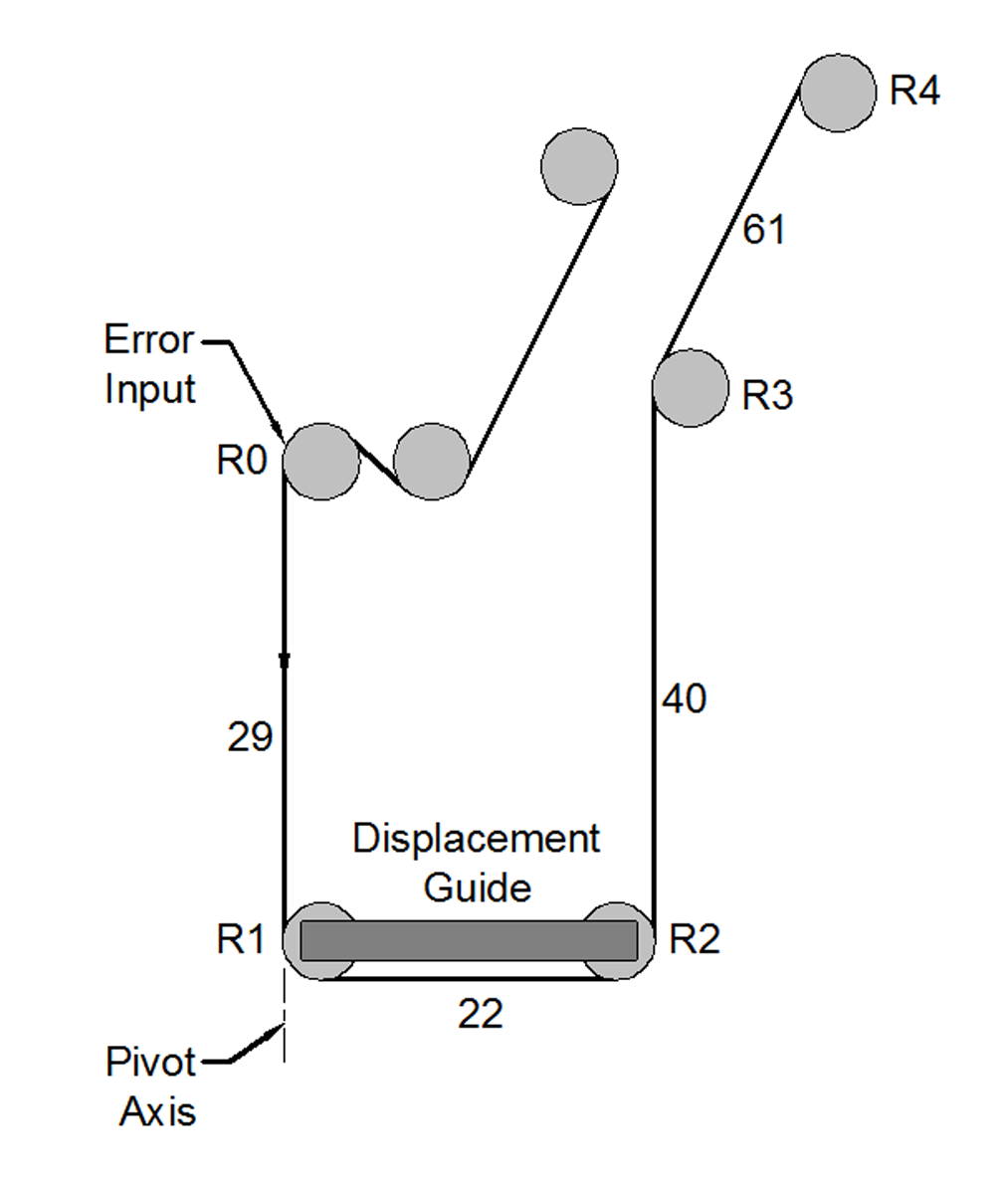
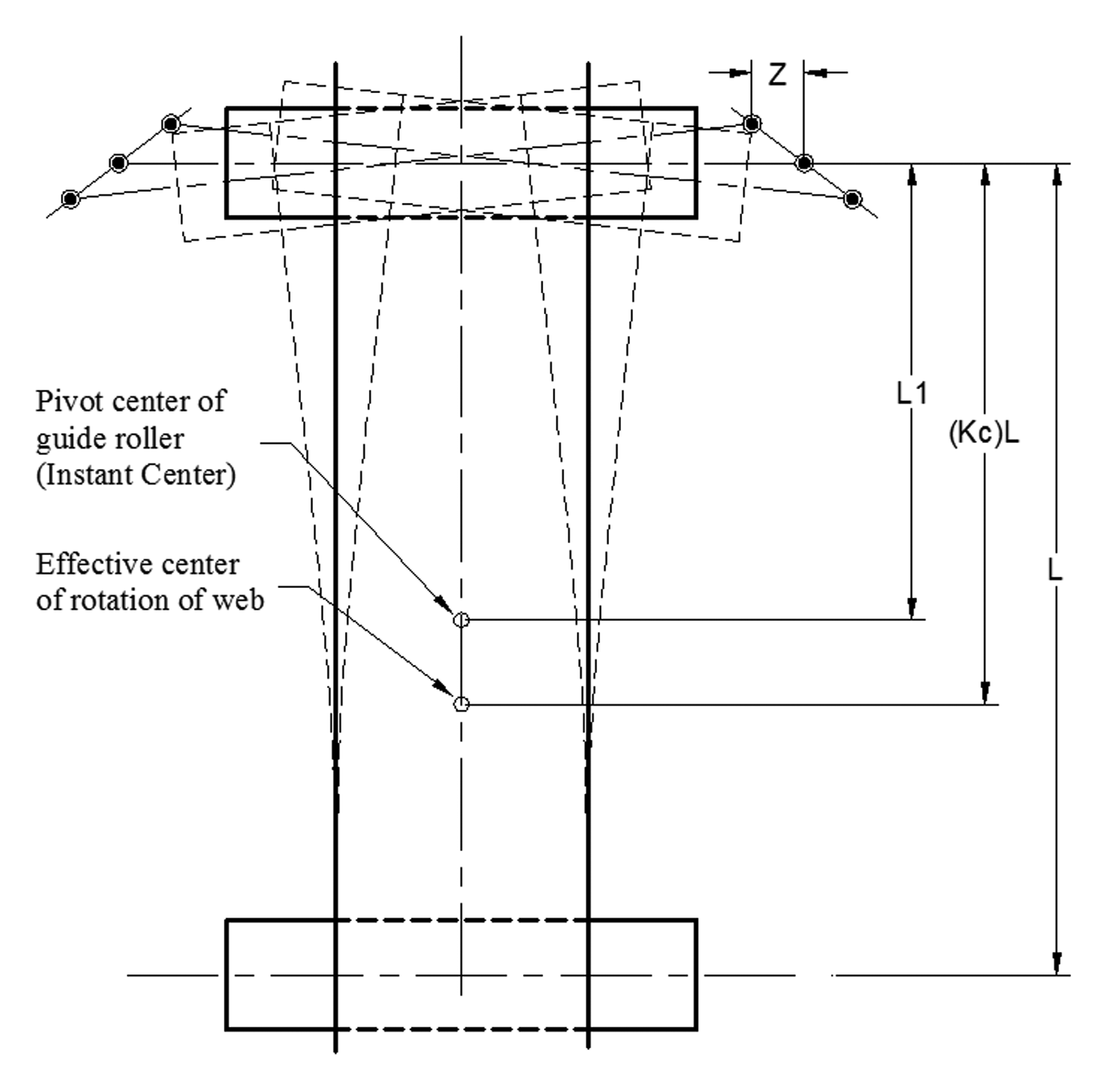
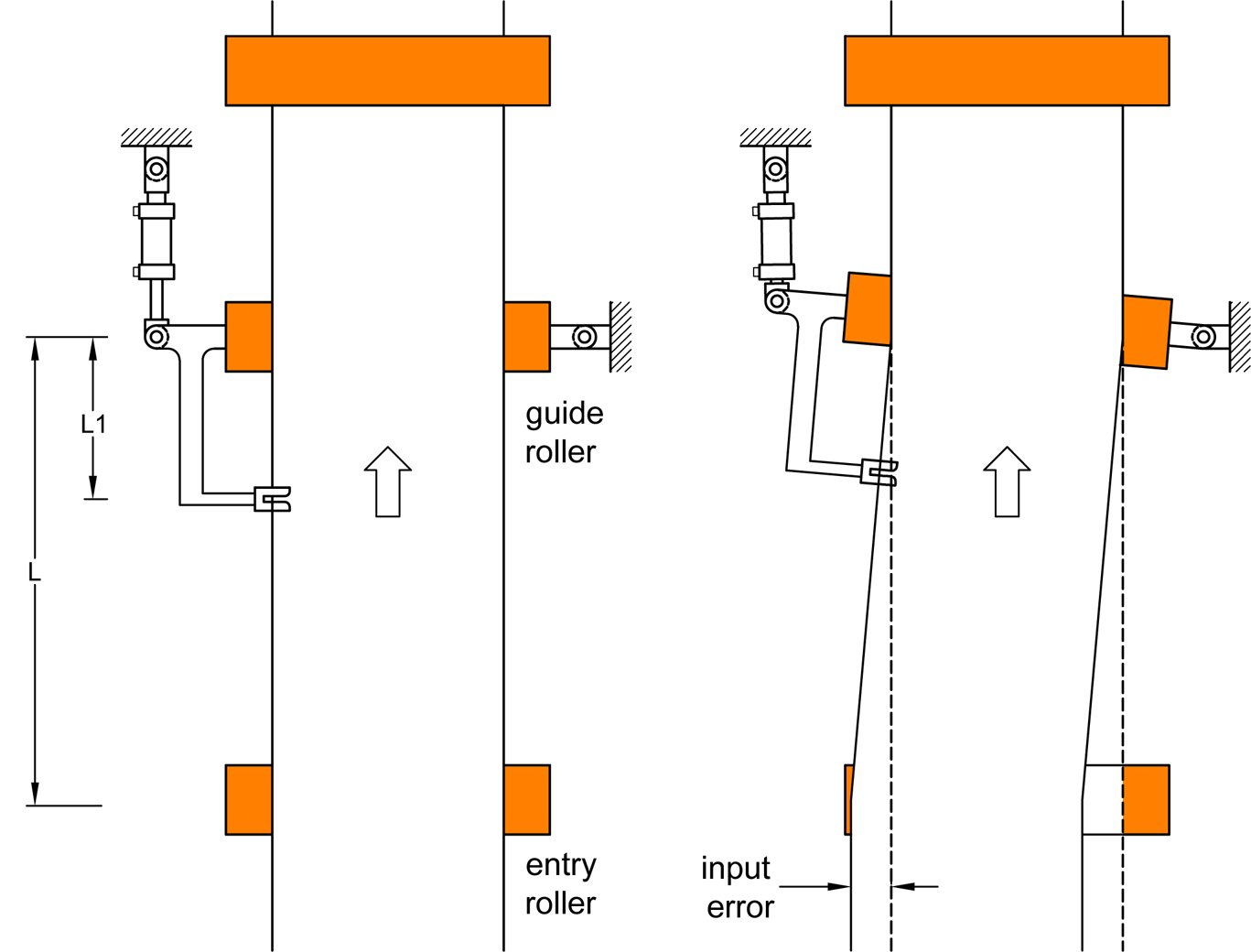
Controlling Web Position With an End-Pivoted Roller AIMCAL 2014 PowerPoint Paper

My interest in controlling lateral position was reawakened by a 1967 Fife memorandum that I found while packing for a move back to Oklahoma in 2013. In it, John Shelton explains a clever method for applying an end-pivoted guide. It involved attaching the sensor to the pivoting roller bracket and locating it in the entering span. This is something I had completely forgotten about. As I read it again, 46 years later, it occurred to me that explaining the problems of end-pivoted rollers would be a good way to explain some of the mysteries of lateral behavior.

Today, of course, there are better ways to make end-pivoted guides work. For example, a high-performance electromechanical guide can use an electronic sensor to provide the position feedback needed to stabilize the guide. It is not my purpose, however, to discuss the state of the art of web guiding. The applications described here are presented only for the purpose of illustrating the fundamental principles of lateral behavior.

Getting and Losing Traction AIMCAL 2012 PowerPoint Paper

The paper begins with a description of the test setup, followed by a review of basic air lubrication principles. Then, the test results for three different rollers (plain, microgroove and spiral groove) are presented and discussed.

Two-Dimensional Behavior of a Thin Web on a Roller - Part 2 IWEB 2011 PowerPoint Paper

This paper presents a continuation of work described at the 2009 IWEB conference in a paper titled, “Two-dimensional Behavior of a Thin Web on a Roller”. The 2009 paper focused primarily on web behavior as it enters onto a roller. In Part 2, a latex web, operating at large strain, is used to make microslip visible in a variety of experiments that shed light on behavior in other parts of the wrap.

Recent work has caused me to have doubts about the lateral slip criterion described here. I intend to revisit this subject in a paper now being prepared for the 2017 IWEB Conference.

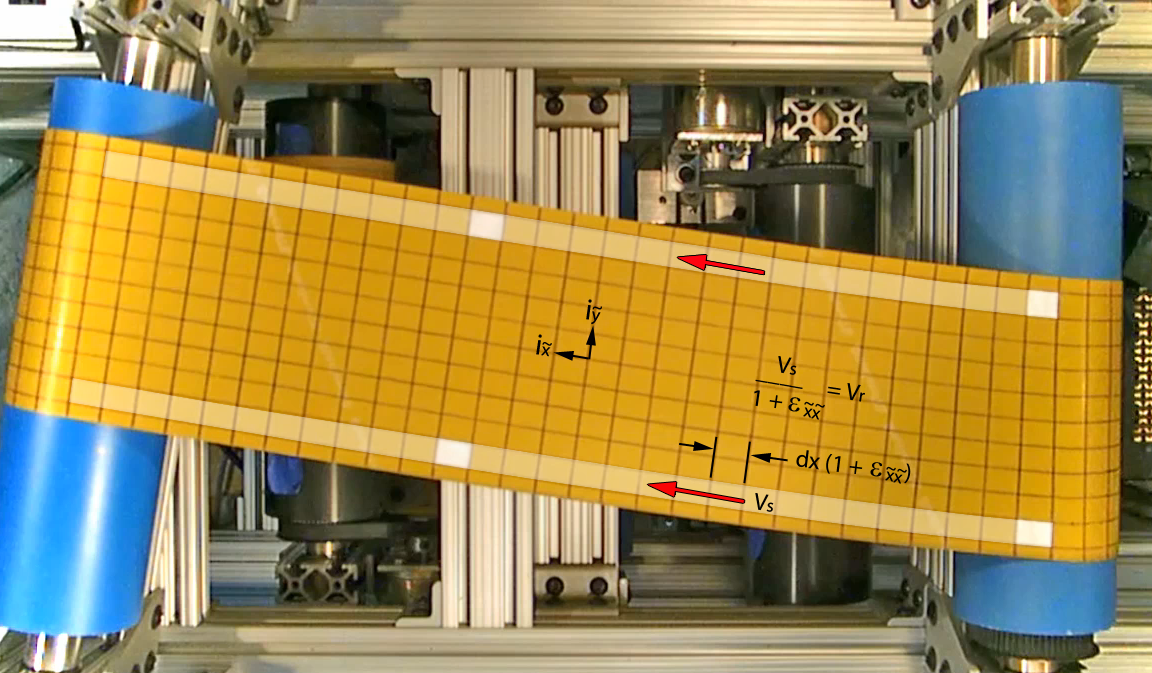
The Use of Conservation of Mass in Modeling Lateral Behavior in Moving Webs IWEB 2011 PowerPoint Paper

Elasticity theory is the obvious candidate for two-dimensional and three-dimensional modeling. Unfortunately, it is viewed by many as a last choice because it requires the use of partial differential equations that can only be solved numerically. This is not the problem it once was. FEA software is now so fast and versatile that it can be used interactively. A method for using elasticity theory is described in my 2005 IWEB paper, “A New Method for Analyzing the Deformation and Lateral Translation of a Moving Web”. It shows how to set up and solve a wide range of lateral behavior problems. A key boundary condition for the method, called the normal strain rule, relies on conservation of mass. This paper shows that the normal strain rule is a special case of a more comprehensive concept that provides a framework for solving a broader scope of problems than contemplated in 2005, especially those in which the relaxed web is not flat. It also introduces a computationally efficient method for implementing this concept by treating all webs, flat or otherwise, as membranes in a two-dimensional frame of reference.

The baggy web model presented at the end of the paper is conceptually correct, but there is an error in the method used to "flatten" the web that invalidates the conclusions concerning baggy web behavior. A corrected version will be posted in the near future.

Taping Rollers for Traction and Spreading AIMCAL 2010 Powerpoint Paper

Line operators commonly apply tape to rollers to spread the web. The most common technique is to put a band of masking tape underneath the web at each edge. A less common method is to use a lateral pattern consisting strips of different length in a chevron-like pattern extending from each roller edge into the web. In both cases, the idea is to approximate a concave profile (concave rollers spread the web).

This paper focuses on the lateral taping method. A number of interesting measurements were made from which some tentative, but useful, conclusions can be drawn.

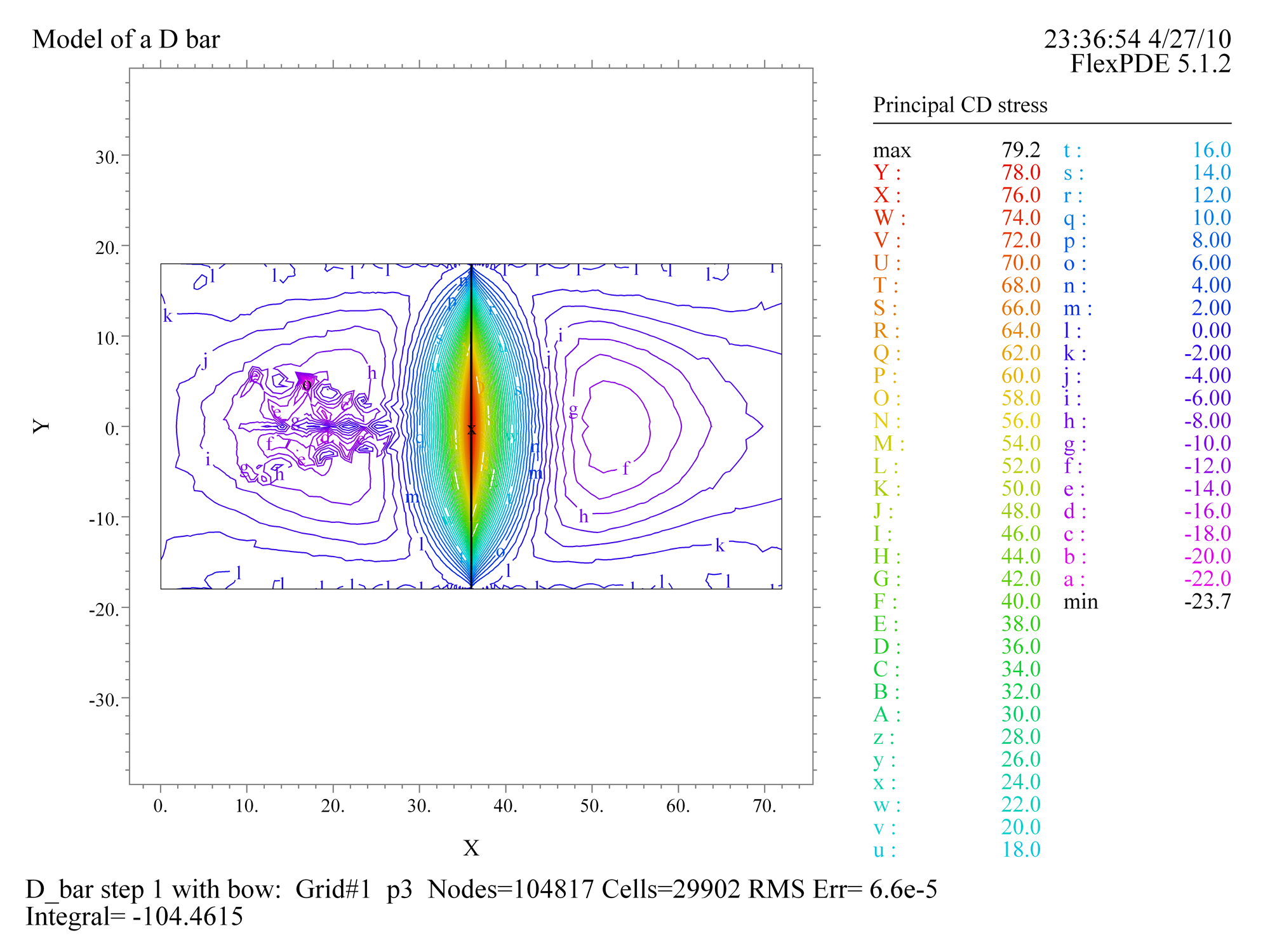
Is There Any Science for D-Bars and Bent Pipes? AIMCAL 2010 PowerPoint Paper

D-bars and bent pipes (non-rotating support bars with straight or curved axes) have received very little attention from web handling analysts. This is partly because their operation seems intuitively obvious. But, are they as simple as they seem? In this paper I answer the following questions.

Do D-bars really spread webs?
Do bowed D-bars produce positive CD spreading stress?
Do straight D-bars spread web and if so, how?
Are there side-effects to be avoided?
Where should D-bars be located for best results?
Do their effects persist very far downstream?
How much bow is needed?

Two-Dimensional Behavior of a Thin Web on a Roller IWEB 2009 PowerPoint Paper

A web on a roller is usually modeled as a one-dimensional belt in a state of pure circumferential stress. However, most of the important problems in lateral web behavior involve shear stress and cross web stress. Furthermore, these stresses, as well as machine direction stress, are often nonuniform. Some work has been done for particular cases using continuum mechanics software. But there are no two-dimensional models that capture the relevant physical principles in a way that can provide a general basis for calculation and insight. Some of the issues that might be addressed with such a model are:
1. Localized loss of traction due to nonuniform stress
2. The amount of spreading that can be supported on a concave or curved roller
3. Strain transport into the next span
4. Interaction of spans due to loss of traction on part of the roller

In this paper,
1. The two-dimensional equations of equilibrium for a thin web on a roller are developed from first principles, taking into account cylindrical
roller geometry and the effects of friction between the web and roller.
2. The questions listed above are explored by experiment and FEA analysis.
3. A method is developed for determining the conditions that must be met at the entry to a roller to insure that cross-web stress gradients
don't cause slipping - for example on concave rollers.

Anatomy of a Wrinkle AIMCAL 2008 PowerPoint Paper PowerPoint_with_notes

In this paper, each step of wrinkle formation is studied using stop-motion photography. This is done on a lab machine specially constructed for this type of study. The machine can handle a latex web operating at large strains, so that the web deformation may be directly observed. It can also be run at very slow speed for observation and then stopped gently for photos.

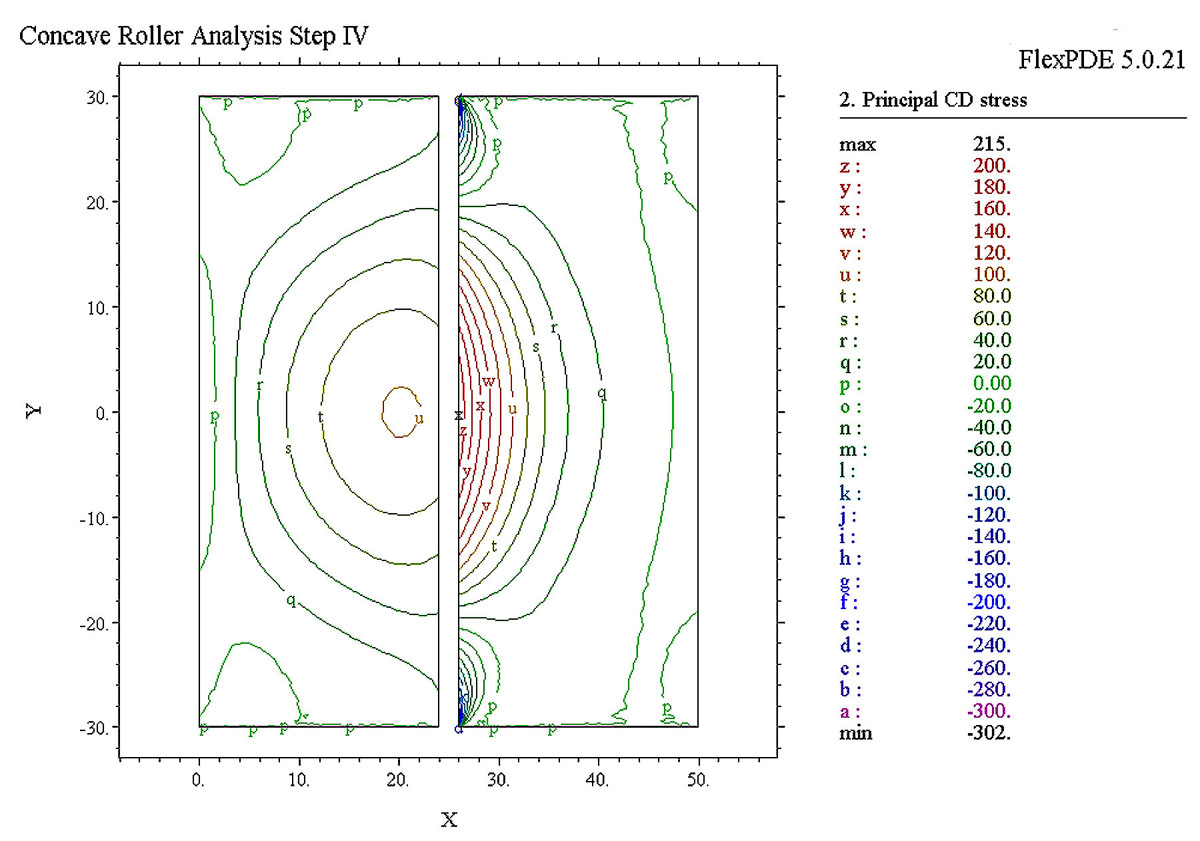
What FEA Analysis Can Tell Us About Spreaders AIMCAL 2008 PowerPoint Paper

Concave and curved rollers are known to be effective spreaders and are commonly used in web processes. However, they are often misunderstood and misapplied. This presentation will use FEA graphics to show how they work and to illustrate limitations in their application.

Behavior of a Thin Flexible Twisted Web IWEB 2007 PowerPoint Paper

This paper describes a twisted web model based on nonlinear elasticity theory. It incorporates the following features.
1. It allows analysis of the effects of rollers that have both in-plane and out-of-plane misalignment, including large rotations.
2. Since the equations of equilibrium for the in-plane stresses are similar to those used in “A New Method for Analyzing
the Deformation and Lateral Translation of a Moving Web” , this model is a natural extension of that work.
3. It incorporates the normal entry and normal strain boundary conditions for the downstream roller
4. It is based on a mathematically rigorous application of nonlinear elasticity theory capable of accounting for the effects of arbitrarily large rotations.

Seeing the Invisible: The Deformations and Stresses that Move Webs AIMCAL 2006 PowerPoint Paper
and the Two Rules that Govern Them.

Web defects such as wrinkles and lateral misalignment are easy to see. However, the deformations and stresses that cause them are usually invisible to the unaided eye. This makes it very difficult for web handling engineers to relate cause and effect. As a consequence, there is still much controversy and confusion over issues such as,
1.    Where do wrinkles come from and what can you do about them if they occur?
2.    What causes a web to track laterally on a misaligned roller?
3.    Should a concave roller be used for spreading instead of a bowed roller?
4.    Does a concave roller even spread?
5.    Should rollers be rough or slick to get rid of wrinkles?
This paper provides insight into these and other web handling issues through the use of a latex web operating at large strains and with graphic illustrations. It will be shown that there are two basic rules that govern a web as it enters onto a roller and that they can be applied to explain what happens at rollers regardless of whether they are tapered, curved, concave, convex or misaligned.

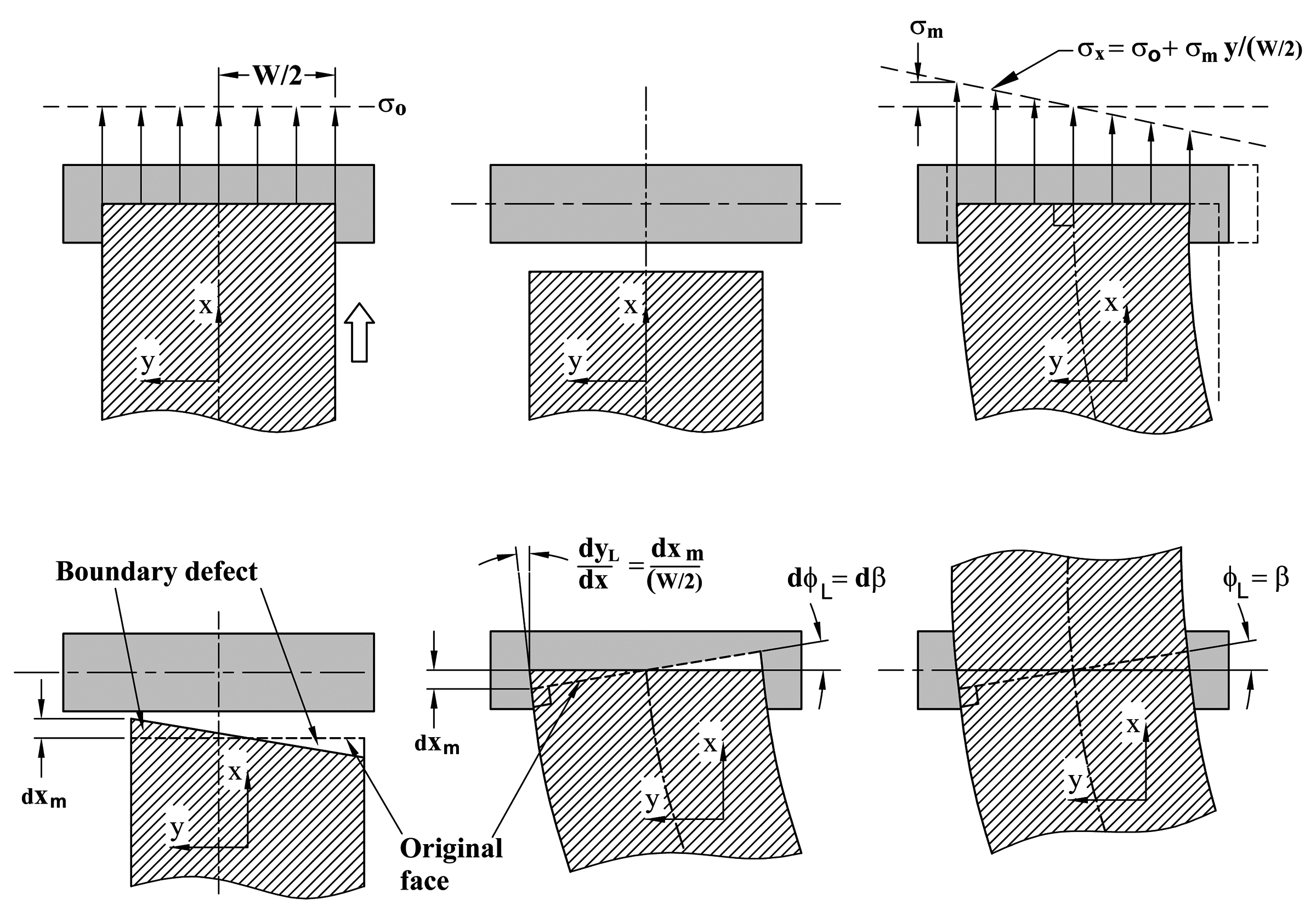
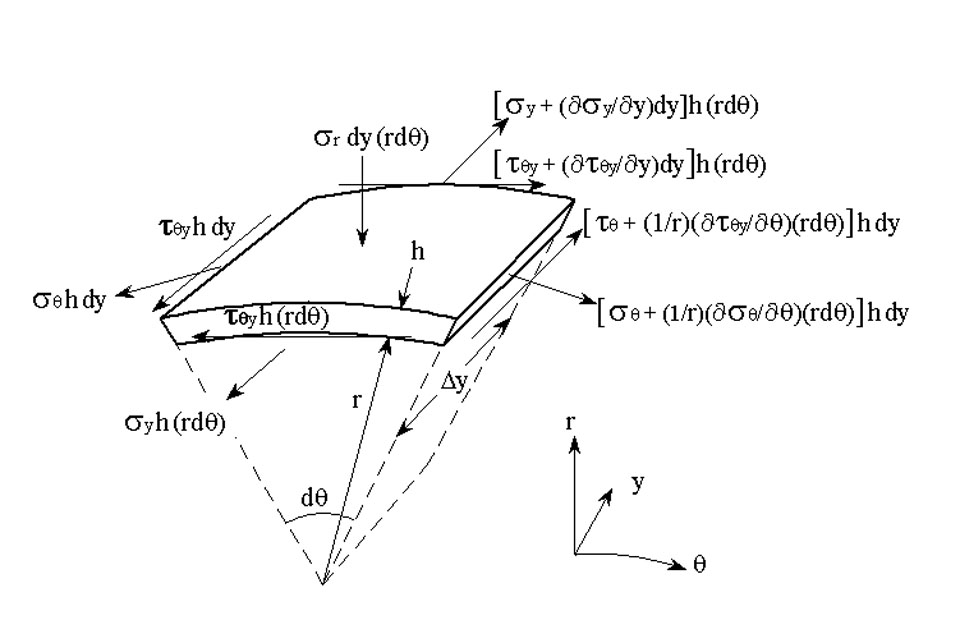
A New Method for Analyzing the Deformation and Lateral Translation of a Moving Web IWEB 2005 PowerPoint Paper

A new method is presented for modeling the lateral elastic behavior of webs. In addition to producing detailed descriptions of stress fields, it provides a new way of looking at problems that will help web process engineers form a better physical picture of web behavior.

The new method is based on nonlinear elasticity theory and employs two fundamental boundary conditions that define web behavior at the point of entry of the web onto a downstream roller. One is a generalization of an existing geometric concept called the normal entry rule. The other, presented here for the first time, is based on application of the principle of conservation of mass. For reasons that will become apparent, it is called the normal strain rule. This paper will show that these two rules, together with a nonlinear version of the equations for two-dimensional plane stress enable the solution of a large class of unsolved web handling problems. Numerical solutions are calculated with a finite-element partial differential equation solver.

Results are shown to be in excellent agreement with experimentally verified data from John Shelton's thesis.

Effects of Concave Rollers, Curved-Axis Rollers and Web Camber IWEB 2005 PowerPoint Paper Note_on_Normal Strain Rule
on the Deformation and Translation of a Moving Web

The new method of analysis is applied to three problems that have resisted detailed

solution. These are:

1. Concave roller

2. Curved-axis roller

3. Cambered web (Curvature of the relaxed web along its longitudinal axis)

Propagation of Longitudinal Tension in a Slender Moving Web IWEB 1999 PowerPoint Paper

This paper presents a model for longitudinal tension propagation in a narrow web. There have been numerous investigations of transverse (out-of- plane) oscillations in a closely related application known as the "Traveling String". A few of these papers included consideration of the longitudinal oscillations which accompanied transverse oscillations. However, no attention has been given to longitudinal tension propagation as a principle feature of solid material transport.
The model is based on the one-dimensional wave equation, modified for a moving medium. Boundary conditions are developed that, for the first time, incorporate tension transfer and mass transport on rolling supports. A closed-form solution is developed using Laplace transforms.